As, we have studied in section 1.3 that in case of reversible Carnot cycle working between temperature T2 and T1,
q₂-q₁/q₂ = T₂ – T₁ / T₂ or 1 – q₁/q₂ = 1 – T₁/T₂
q₁/T₁ = q₂/T₂ …(i)
where q₂ is the amount of heat absorbed isothermally and reversibly at temperature T₂ and q₁ is the amount of heat lost isothermally and reversibly at temperature T₁,
The equation(i) in its general form may b erepresented as ;
qrev/T = constant
where qrev is the quantity of heat absorbed or evolvedin aprocess carrried out reversibly at a temperature T.
The quantity qrev / T, as we shall aee represents a definite or a state function, viz., the entroopy change of the system.
If heat absorbed (q₂) is given a ppositiv esign an dheat lost(q₁) i sa given a negative sign , equation (i) becomes
+ q₂/T₂ = – q₁/T₁ or q₁/T₁+ q₂/T₂ = 0
Σ q / T = 0 …(ii)
Thereffore, when isothermal and adiabatic processes in a carnot cycle are carried out reveribly (i.e, infinitesimally slowly), the summation of q/T terms is equal to zero.
Any reversible cyclic process can be shown to be made up of a series of carnot cycle .let us considered a reversible cyclic process ABA in which the change from A to B and back to stae A ( Fig. 1.3) i scarried out reversibly. Fig 1.3 shows the cycle ABA to be made up of a number of carnot cycles, i.e, of a series of isothermal and adiabatics . The lines slanting horizontally represents adiabatics while those lines slanting vertically represents isothermals of small carnot cycles . If each Carnot cycle is made extremely small by increasing their number, it can be made to correspond more closely to continous curve ABA. In such case ,any reversible cycle can be supposed to made up of an infinite number of carnot cycles.
But for each cycle,
q₁/T₁ + q₂/T₂ = 0 …(iii)
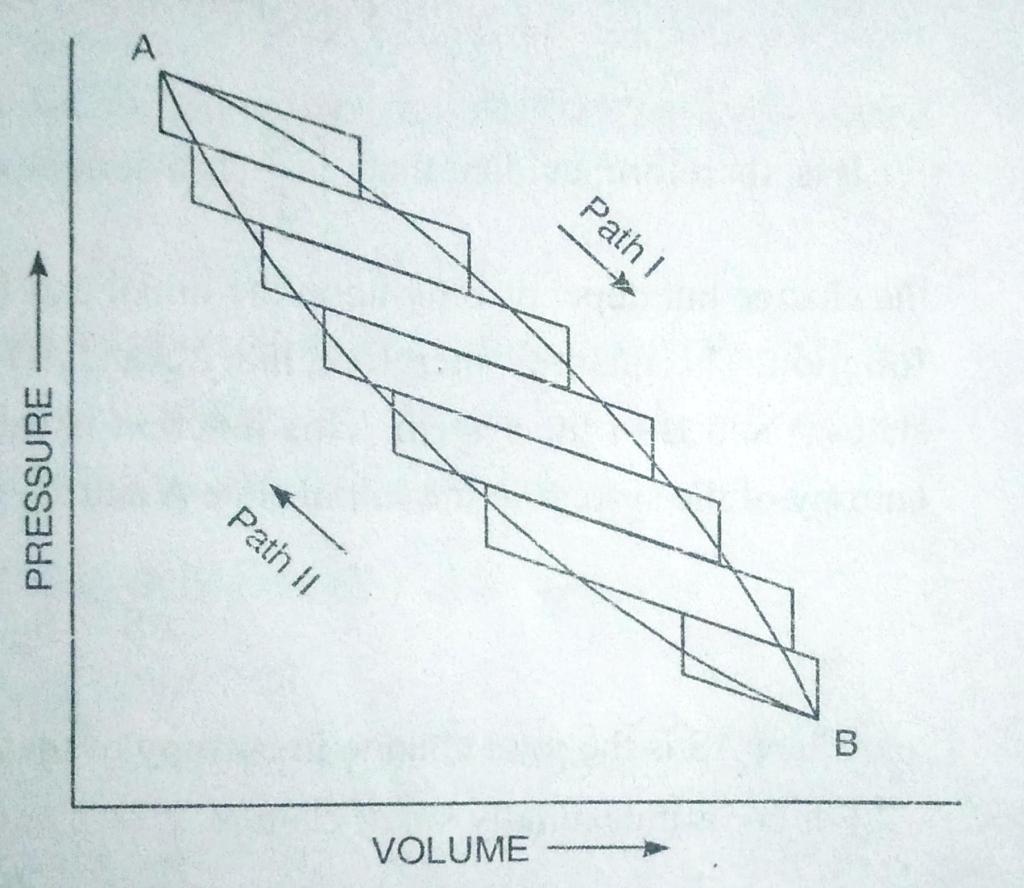
Therefore , for the reversible cycle ABA which consist of series of carnot cycles, the above expression can be expressed as,
Σ dq/T = 0
In case,m the changes are infinitesimally small, thenth eabov eequation can be expressede as
Σ dq/T = 0
Since the given cycle is performrd in two steps , viz.,from A to B and back from B bto A, therefore,
Σ dq/T = A∫B dq/T + B∫A dq/T = 0 . …(iv)
where B∫A dq/T represents the summation of all the dq/ T terms when the change occurs from A to B via path I and A∫B dq/T represents the summation of all dq/T terms when the system returns from B to original state A via path II
Evidently from the equation (iv) we have
A∫B dq/T (path I ) = – B∫A dq/T (path II)
A∫B dq/T (path I) = A∫B dq/T (path II)
It is , therefore, evident that A∫B dq/T is a definite quantity which does not depend upon the path followed for the change but depends only upon the initial and final states A and B of the system and, is , therefore, astate function. This quantity, therefore like ΔU and ΔH represemts the change in some singled – valued function of the states A and B of the system. This function is called entropy and is denoted by the symbol S. if SA is the entropy of the system in the initial state A and Sb is the entropy of the system in the final state B, then
ΔS = SB – SA = A∫B dq/T
where ΔS is the total change in entropy of the system in going from initial state A to the final state B.
for an infinitesimally small change
dS = dq/T
But at a constant temperature, for a finite change ΔS and Δq can be replaced by ΔS and q respectively . As such, for a finite change at a constant temperrature.
ΔS = q/T
It is important to mention here that since entropy is a function of state only and is independent of path followed, therefore, the change in entropy in going from initial A to the final state B will invariably be the same whether the change is brought about reversibly or not. but, mathematically, it will be expressed by the expression.
ΔS = A∫B dq/T
only when the change has been brought about reversibly. this is because the above equation has been derieved from carnot cycle in which all the changes are brought about in a reversible manner.
It is not easy to define the actual entropy of the system. However, it is more convenient to define change of entropy of a system.
The change in entropy of a system may be defined as the integral of all the terms involving heat absorbed (q) divided by the absolute temperature (T) during each infinitesimally small change of the process carried out reversibly.
Thus, for a change at constant temperature,
ΔS = qrev/T
Thus, in simple words, the entropy change may also be defined as the quantity of heat absorbed isothermally and reversibly divided by the absolute temperature (T) at which heat is absorbed.
UNITS OF ENTROPY.
Change in entropy (ΔS) is expressed as
ΔS = qrev/T
Therefore, units of entropy should be expressed as calories per degree i.e., Cal deg-1. This is also called entropy unit.
SI UNITS.
SI units of entropy, accordingly, should be joules per degree kelvin (JK-1)
Since entropy is an extensive property, its value should depends upon the quantity of the substance involved. Generally, its expressed for one mole of the substance. Hence depending upon the unit of heat, the unit of entropy are either expressed as calories per degree per mole or joules per kelvin per mole.
Tell us how we are doing by star rating above.

“I strongly believe that the power of food has a fundamental place in people’s homes that binds us to the best things of life.”
— Lakin Smith


